O que é a taxa de variação média?
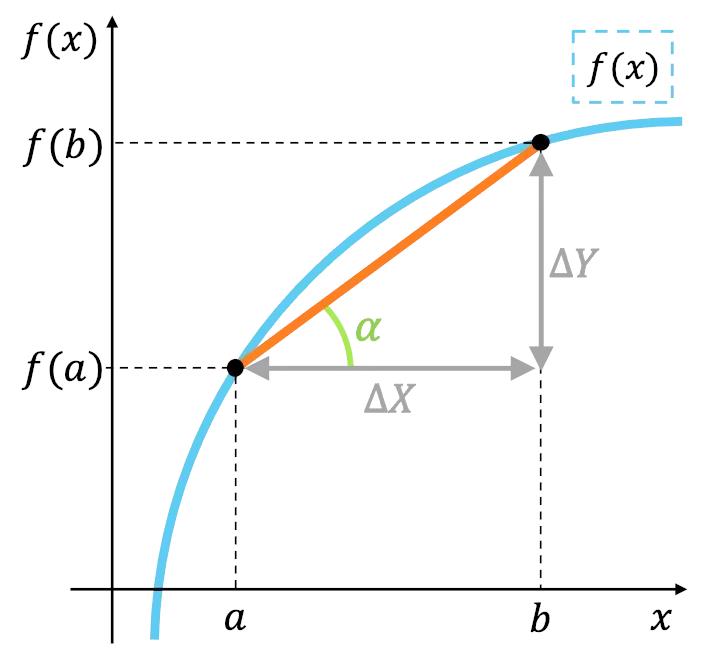
A taxa de variação média (T.VM.) de uma função durante um intervalo fechado mede o aumento ou a diminuição dessa função durante o mesmo intervalo. Em outras palavras, estamos analisando o quão íngreme ou "íngreme" a inclinação está em uma seção da função. Medimos o quanto y aumenta dividido pelo quanto x varia em uma parte específica da função.
Como calcular a TVM de uma função f(x) em um intervalo [a, b] (versão fácil)
Como já vimos, a taxa média de mudança é o quanto f(x) ou "y" aumenta ou diminui em relação a "x". Ou seja, um quociente. Sua fórmula é a seguinte:
TVM [a, b] = (f(b) - f(a)) / (b - a)
Truque para memorizar a fórmula: Pense na palavra "baba" ou "Alibaba". Então você saberá que o b vem antes do a no numerador e denominador.
Agora suponha que nos pedem para calcular a TVM da função f(x)= x^2-x+3 no intervalo [2, 3]. Isso seria resolvido da seguinte forma:
- Identificar o que é a e o que é b.
- Encontre o valor de f(b).
- Encontre o valor de f(a) (não importa se você faz o passo 2 primeiro e depois o passo 3).
- Inserir os valores na fórmula e resolver.
Passo 1: Se formos solicitados a calculá-lo em um intervalo [a, b], o valor à esquerda é a e o valor à direita é b. Portanto, a é igual a 2 e b é igual a 3.
Passo 2: Encontramos o valor de f(b) inserindo o valor de b na função e resolvendo:
f(3) = 3^2 - 3 + 3 = 9 - 3 + 3 = 9
Passo 3: Nós fazemos o mesmo com f(a):
f(2) = 2^2 - 2 + 3 = 4 - 2 + 3 = 5
Passo 4: Inserimos resultados em nossa fórmula e operamos:
(f(b) - f(a)) / (b - a) = (9 - 5) / (3 - 2) = 4 / 1 = 4
A TVM da função f(x) = x^2 - x + 3 no intervalo [2, 3] é 4.
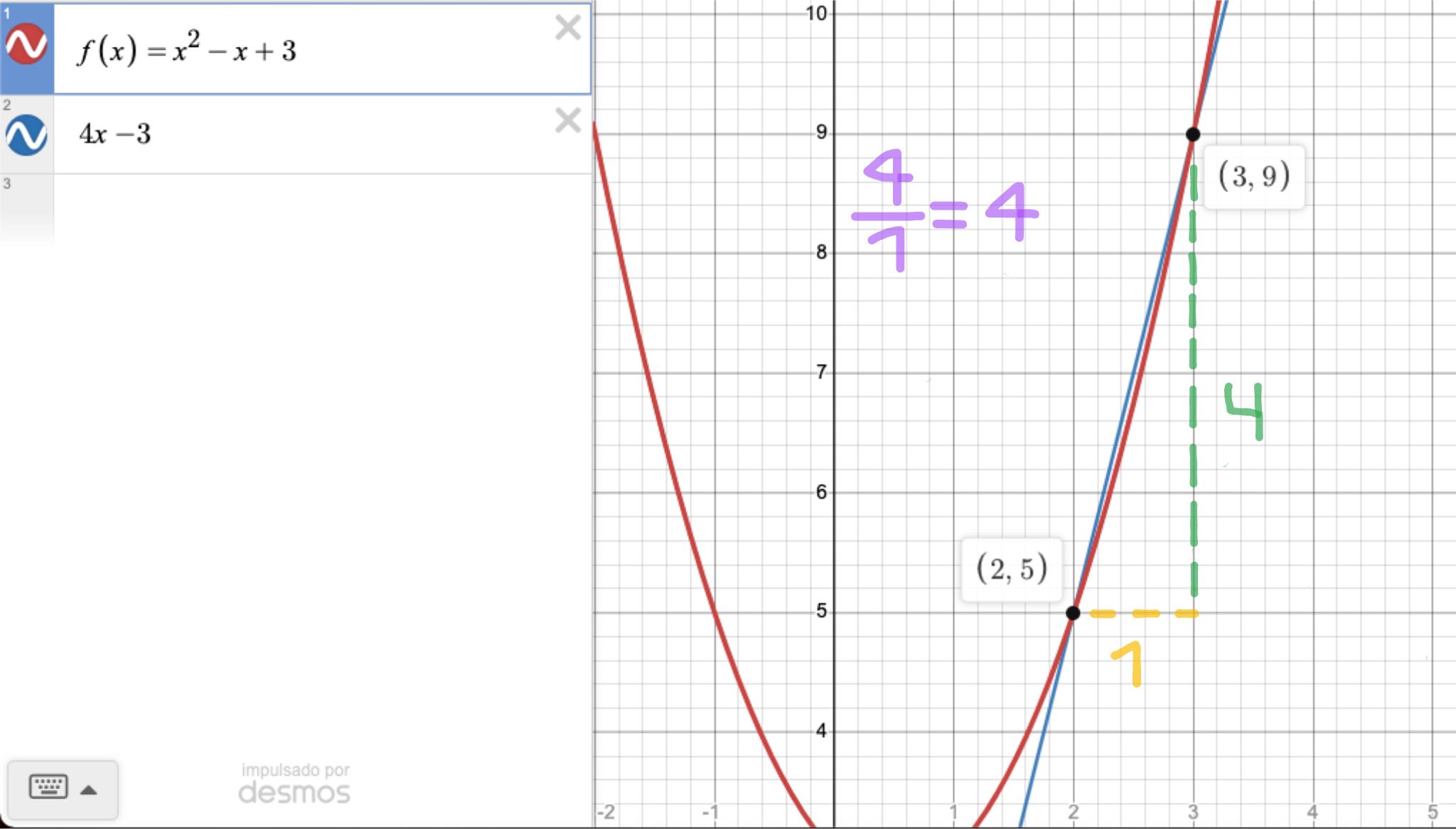
Demonstração gráfica
Podemos observar o aumento da função a partir dos pontos (2, 5) e (3, 9). A linha vermelha é a função e a linha azul é a inclinação que passa através dos dois pontos do intervalo (linha tangente), que é equivalente à inclinação da função. Esta linha é a função f(x) = 4x - 3, portanto tem um incremento de 4 em relação a x.
Você pode ver como para cada unidade que a função avança no eixo x, a função avança 4 unidades no eixo y. É como se para cada gol que você marca você ganhasse quatro cupcakes.
Nossa função moveu uma unidade horizontalmente (de 2 a 3) e quatro unidades verticalmente (de 5 a 9). Tudo no intervalo fechado [2, 3].
A TVM de uma função f(x) em um intervalo [a, a + h] (versão difícil)
Agora que vimos como é a TVM com um intervalo fechado [a, b], vamos ver como é feito com um intervalo [a, a + h].
Há duas diferenças principais.
A primeira é que estamos lidando com um desconhecido/variável, h, portanto o resultado do M.V.T. também conterá a variável h. Isto pode ser confuso, mas é assim. Como h é variável, o resultado em que h aparece também será variável.
A segunda implica que teremos que inserir não apenas um número, mas uma soma de uma letra e um número (a + h) na operação. Aqui teremos que ter cuidado ao inserir os valores, pois se o fizermos muito rapidamente ou se nos perdermos, podemos perder sinais negativos ou poderes. Erros como estes podem lhe custar todo o exercício em um exame.
Desta vez, a fórmula é quase a mesma. Somente f(b) é alterado para f(a + h):
T.V.M. ([a, a + h]) = (f(a + h) - f(a)) / (f(a + h) - f(a)).
Dito isto, vamos calcular a T.V.M. da função f(x) = x^2 - x + 3 no intervalo [2, 3]. O mesmo que no exercício anterior. Seguiremos as mesmas instruções:
- Diferencie a de um + h. Isto já é dito pelo intervalo, por isso vou pular este passo.
- Encontre o valor de f(a).
- Encontre o valor de f(a + h). Como precaução, inserir sempre "a + h" entre parênteses.
- Substituir as funções pelos resultados que obtivemos e operamos.
Passo 2: Substituir em f(x) o valor de a pelo valor de x e operar:
f(2) = 2^2 - 2 + 3 = 4 - 2 + 3 = 5
Passo 3: Substituir em f(x) o valor de a + h pelo valor de x e operar. Colocar um + h entre parênteses:
f(2 + h) = (2 + h)^2 - (2 + h) + 3 = (4 + 4h + h^2) - 2 - h + 3 = h^2 + 3h + 5.
Passo 4: Colocamos nossos resultados na fórmula e operamos:
(f(a + h) - f(a)) / ((a + h) - a)) = (h^2 + 3h + 5) - 5) / (2 + h) - 2 = (h^2 + 3h) / h = (h + 3) / 1 = h + 3.
A TVM é h + 3. Este é o resultado final; não há mais etapas. O resultado se aplica a qualquer valor de h.
Se você estiver confuso, assuma que h é igual a 1. Vá para a demonstração gráfica de antes e você verá que se h é igual a 1. h seria a distância entre 2 e 3:
f(2 + h) = f(3) -> h^2 + 3h + 5 = (1)^2 + 3(1) + 5 = 9
h + 3 = 4
Questões finais
- Por que é chamado de intervalo "fechado"?
Há dois tipos de intervalos: aberto e fechado. Os intervalos abertos incluem o que está dentro deles, mas não seus dois pontos finais. Os intervalos fechados, por outro lado, incluem seus dois pontos finais.
Exemplo: o intervalo aberto (2, 3) inclui números de 2.0000...1 a 2.9999...9. O intervalo fechado [2, 3] inclui números de 2 a 3.
- Por que "b - a" e não "a - b"?
Porque medimos a variação entre dois pontos (intervalo) medindo o valor do segundo ponto (isto é, b) com relação ao ponto anterior (ponto a). Se fizermos a operação fazendo "a-b", teremos a T.V.M. com o sinal oposto.
Muito obrigado por ler meu artigo! Espero que tenham gostado e que tenham aprendido algo novo. Se quiser que você ou seu filho/filha iniciem o ensino médio com o apoio de um professor particular de matemática, não hesite em entrar em contato comigo ou com outro membro da plataforma.